
> split it ito 2 triangles and use your quadrilateral interpolant at So, when you draw, le's say one quandrangles, you first > completely disconnected even overlapping (I do not say that it's > that triangles that you display in gmsh are not s mesh, they may be > interpolations, we use a recursive algorithm. > can display everything but the only primitives are simplices (points, > Yes, I use here high order finite elements for compressible 3d flows, gmsh > I kindly beg you if you could answer the following questions.

> of a NACA airfoil pressure field on my PC. > Now when there is a Gmsh, I thought that I could produce a coloured picture
#GMSH FILE FLOW AROUND A CYLINDER SOFTWARE#
> Modelling software running on an HP UNIX workstation. > Pre- and post-processing has been handled using I-DEAS Finite Element > I used 2D 8-node superparametric (pressure) and isoparametric (velocity) > laminar flow past a cylinder and a laminar flow past a symmetric NACA > I tried the solver on classical examples of driven cavity laminar flow, > two-dimensional stationary incompressible Newtonian fluid flow. > classical fluid mechanics system of partial differential equations modelling > My name is Robert Jurjevic and some time ago I wrote a solver for a Subject: Re: scalar-quadrangle-value in Gmsh's ASCII post-processing file Nevertheless in my opinion a proper way to do it is to implement the support to scalar-quadrangle-value into Gmsh (imagine that you want to zoom something to extremes, etc.).

I do not know when I will start working on this, but if I will ever and if I finish the program I will pass the C source to you. I intend to write an ANSI C program which will for every accept scalar-quadrangle-value in the input ASCII file generate a corresponding scalar-triangle-value-s in the ASCII output file. White nodes are nodes in which we calculate 4-node quadrangular finite element interpolated pressure values. If the difference (for all red nodes) is small enough (say, that it was in figure 3) there is no need for further subdivisions and we are going back to a previous subdivision and form 3-node triangles as shown in figure 4.įigure 4: Final triangulation of 4-node quadrangular finite element. Red nodes are nodes in which we calculate the difference between linear and 4-node quadrangular finite element interpolated pressure values. If the difference (for all red nodes in figure 2) is not small enough (the difference will be compared to the pressure change on the element) the subdivision should continue as shown in figure 3, where again we calculate the difference between linear and 4-node quadrangular finite element interpolated pressure values in red nodes.įigure 3: 4-node quadrangular finite element with sixteen new 4-node quadrangles.
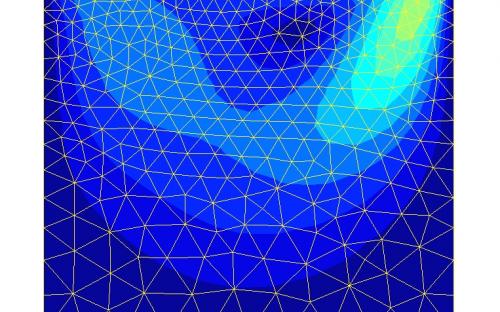

Then, I will calculate the difference between linear and 4-node quadrangular finite element interpolated pressure values in red nodes (see figure 2).įigure 2: 4-node quadrangular finite element with four new 4-node quadrangles. So, when you draw, let's say one quadrangle, you first split it into 2 triangles and use your quadrilateral interpolation at points, Then, if your solution is higher order, you split recursively the triangles into 4 triangles, the recursion stops when your solution is sufficiently linear on the actual triangle.Īctually, I will first divide my 4-node (black nodes) quadrangular finite element into four 4-node quadrangles (figure 1) with five new nodes (white nodes) in which I will calculate the pressure using 4-node quadrangular finite element interpolation.įigure 1: 4-node quadrangular finite element with four new 4-node quadrangles. Previous message: scalar-quadrangle-value in Gmsh's ASCII post-processing file.Scalar-quadrangle-value in Gmsh's ASCII post-processing file Robert Jurjevic robert.jurjevic at .uk Scalar-quadrangle-value in Gmsh's ASCII post-processing file


 0 kommentar(er)
0 kommentar(er)
